Skip to content

Oscillating Membrane

Bessel Functions

In this notebook we are going to make some fun with Oscillating membrane implementing Bessel Functions.

import numpy as np
from scipy.special import jn, yn, jn_zeros, yn_zeros
import scipy as sci
import scipy.special as sp

from __future__ import division

import matplotlib.pyplot as plt
import matplotlib
import pylab
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm, colors
%matplotlib inline
import seaborn as sns
sns.set()

Bessel Functions

n = 0 # order
x = 0.0
# Bessel function of first kind
print("J_%d(%f) = %f" % (n, x, jn(n, x)))
x = 1.0
# Bessel function of second kind
print ("Y_%d(%f) = %f" % (n, x, yn(n, x)))

J_0(0.000000) = 1.000000
Y_0(1.000000) = 0.088257

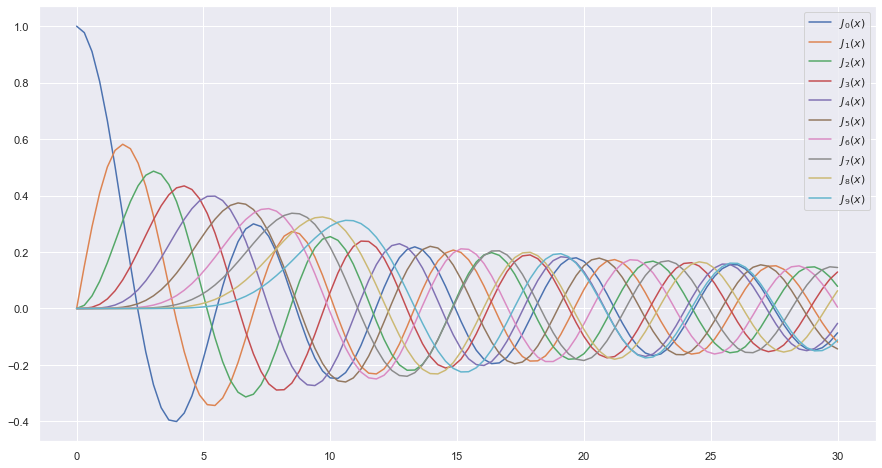
x = np.linspace(0, 30, 100)
plt.figure(figsize = (15,8))
for n in range(10):
    plt.plot(x, jn(n, x), label=r"$J_%d(x)$" % n)
    plt.legend();

png

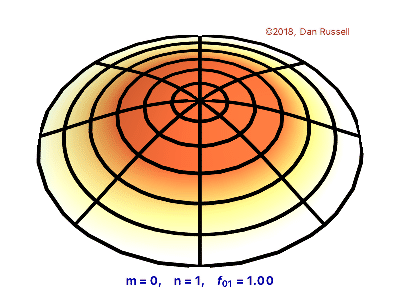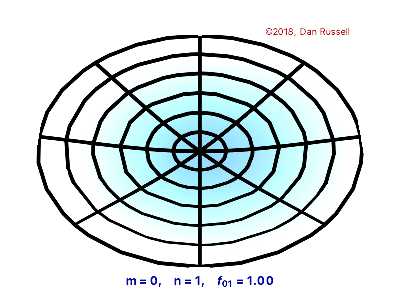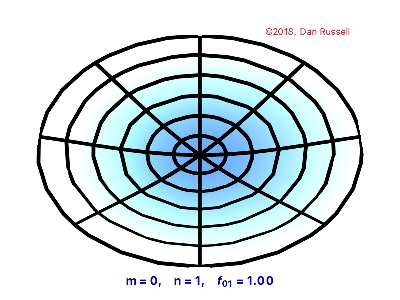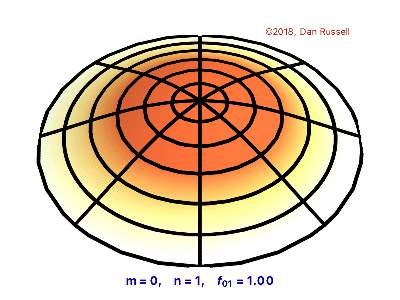
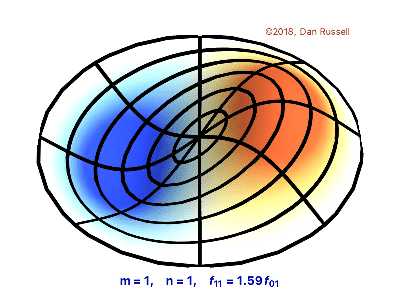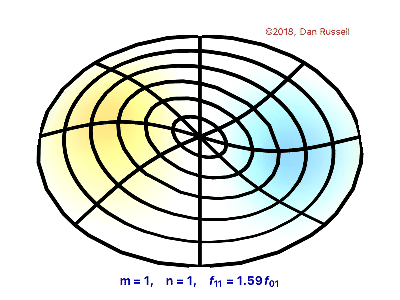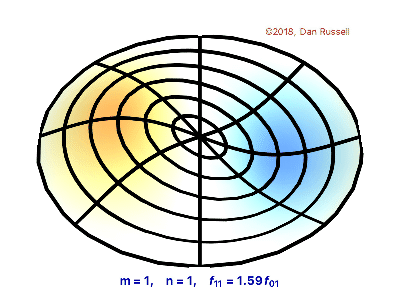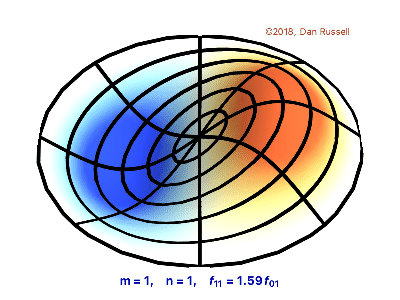
Vibrating Circular Membrane

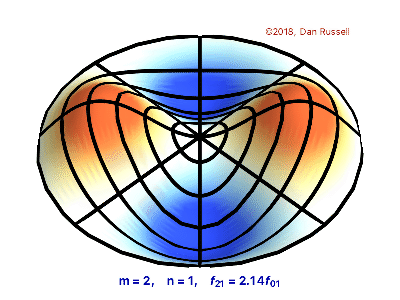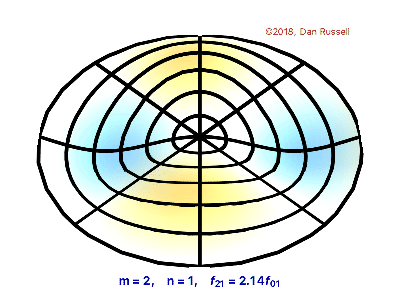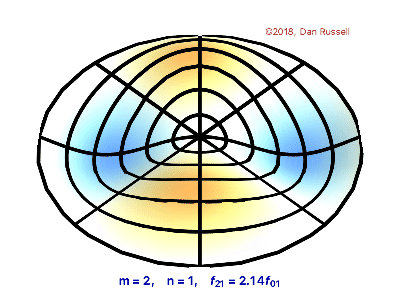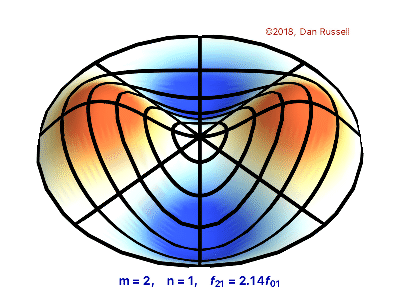
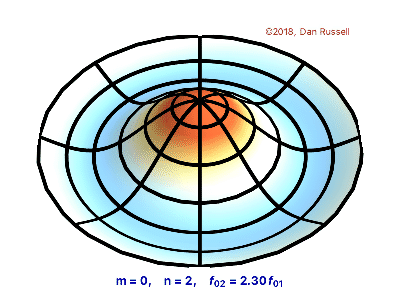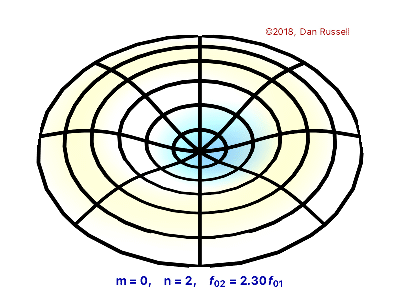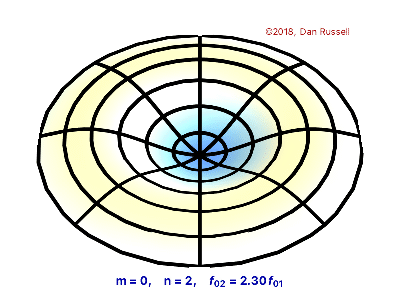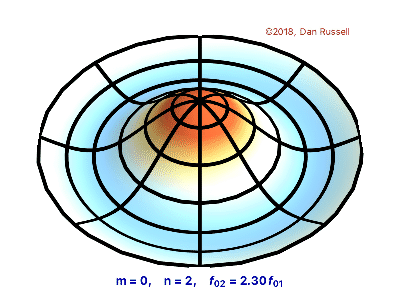
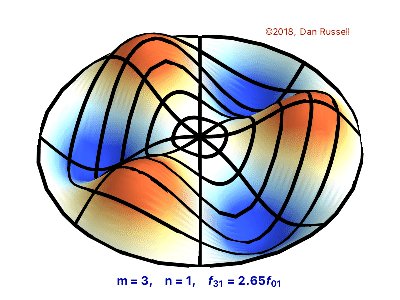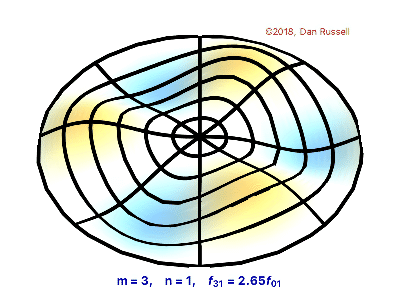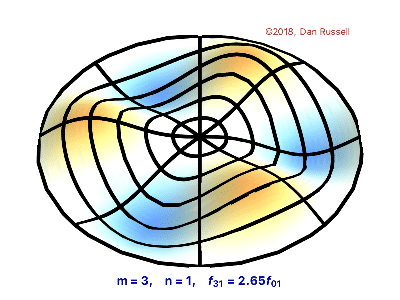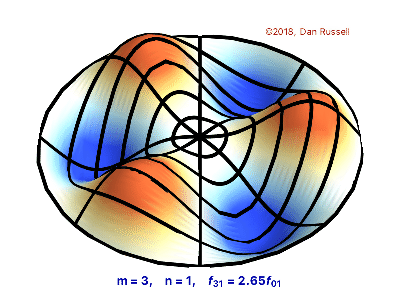
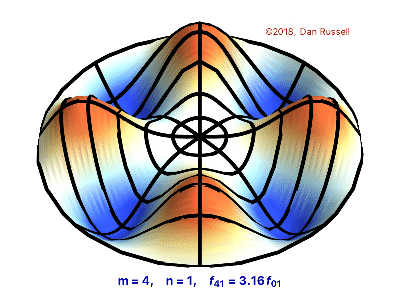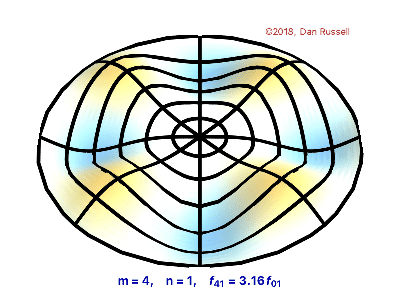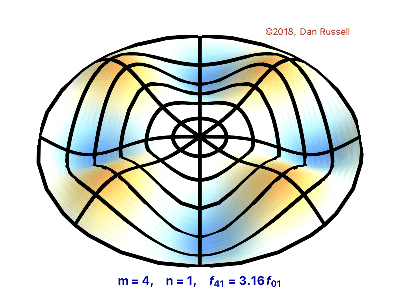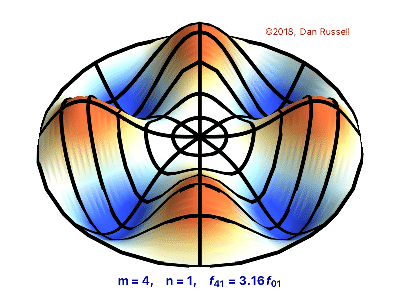
The vibrations of a thin circular membrane stretched across a rigid circular frame (such as a drum head) can be described as normal modes written in terms of Bessel functions:

\( \large{z(r,θ;t)=AJ_n(kr)\sin(nθ)\cos(kνt)}\)

where $(r,θ)$ describes a position in polar co-ordinates with the origin at the centre of the membrane, t is time and v is a constant depending on the tension and surface density of the drum. The modes are labelled by integers $n=0,1,⋯ $ and $m=1,2,3,⋯$ where k is the mth zero of $J_n$.

The following program produces a plot of the displacement of the membrane in the n=3,m=2 normal mode at time t=0.

Table p q
img img img
--- --- ---
img img img
--- --- ---
img img img 
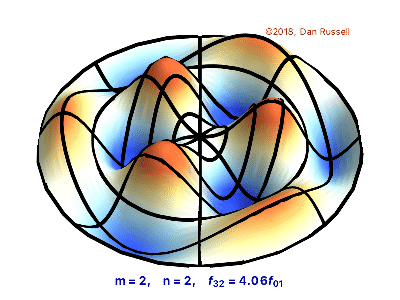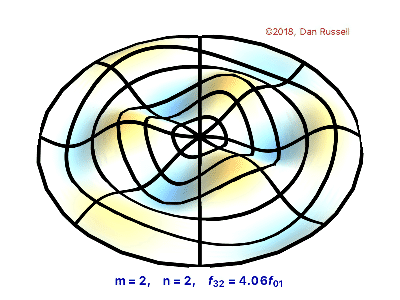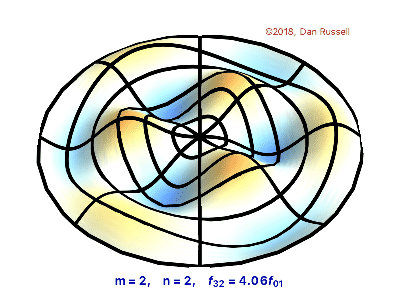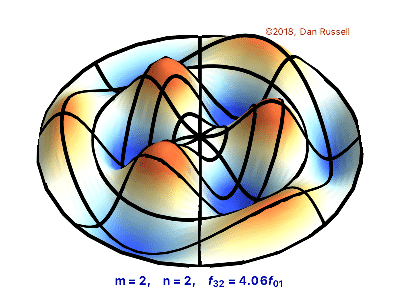def displacement(n, m, r, theta):
    """
    Calculate the displacement of the drum membrane at (r, theta; t=0)
    in the normal mode described by integers n >= 0, 0 < m <= mmax.

    """

    # Pick off the mth zero of Bessel function Jn
    k = jn_zeros(n, mmax+1)[m]
    return np.sin(n*theta) * jn(n, r*k)

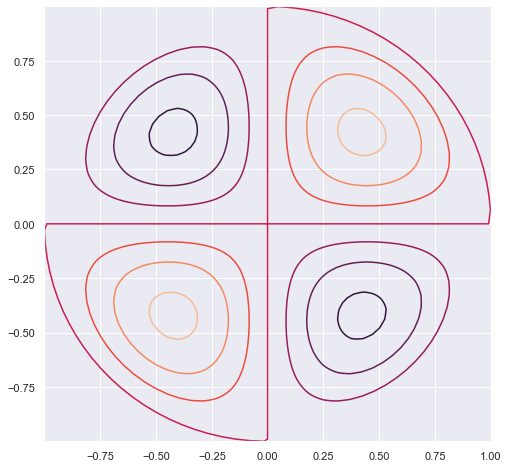
Oscillating membrane ( SIngle Plot, (2,0))

# Allow calculations up to m = mmax
mmax =10
# Positions on the drum surface are specified in polar co-ordinates
r = np.linspace(0, 1, 100)
theta = np.linspace(0, 2 * np.pi, 100)

# Create arrays of cartesian co-ordinates (x, y) ...
x = np.array([rr*np.cos(theta) for rr in r])
y = np.array([rr*np.sin(theta) for rr in r])
# ... and vertical displacement (z) for the required normal mode at
# time, t = 0

n0, m0 = 2,0
z = np.array([displacement(n0, m0, rr, theta) for rr in r])
plt.figure(figsize = [8,8])
pylab.contour(x, y, z)
pylab.show()

png

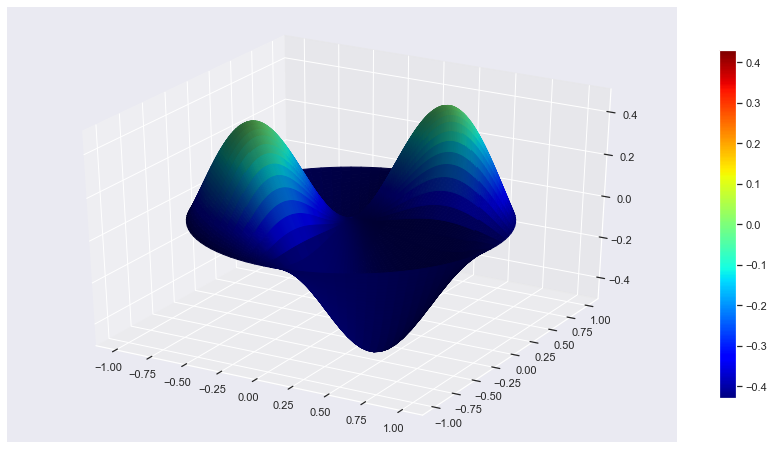
Oscilating Membrane ( Single, 3D plot, (2,0))

r, theta = np.mgrid[0:1:100j, 0:2*np.pi:100j] 
x = r*np.cos(theta)
y = r*np.sin(theta)
z = displacement(n0, m0, r, theta)
N = z/(z.max() -z.min())
fig, ax = plt.subplots(subplot_kw=dict(projection='3d'), figsize=(15,8))
im = ax.plot_surface(x, y, z, rstride=1, cstride=1, facecolors=cm.jet(N))
mm = cm.ScalarMappable(cmap=cm.jet)
mm.set_array(R)    
fig.colorbar(mm, shrink=0.8);

png

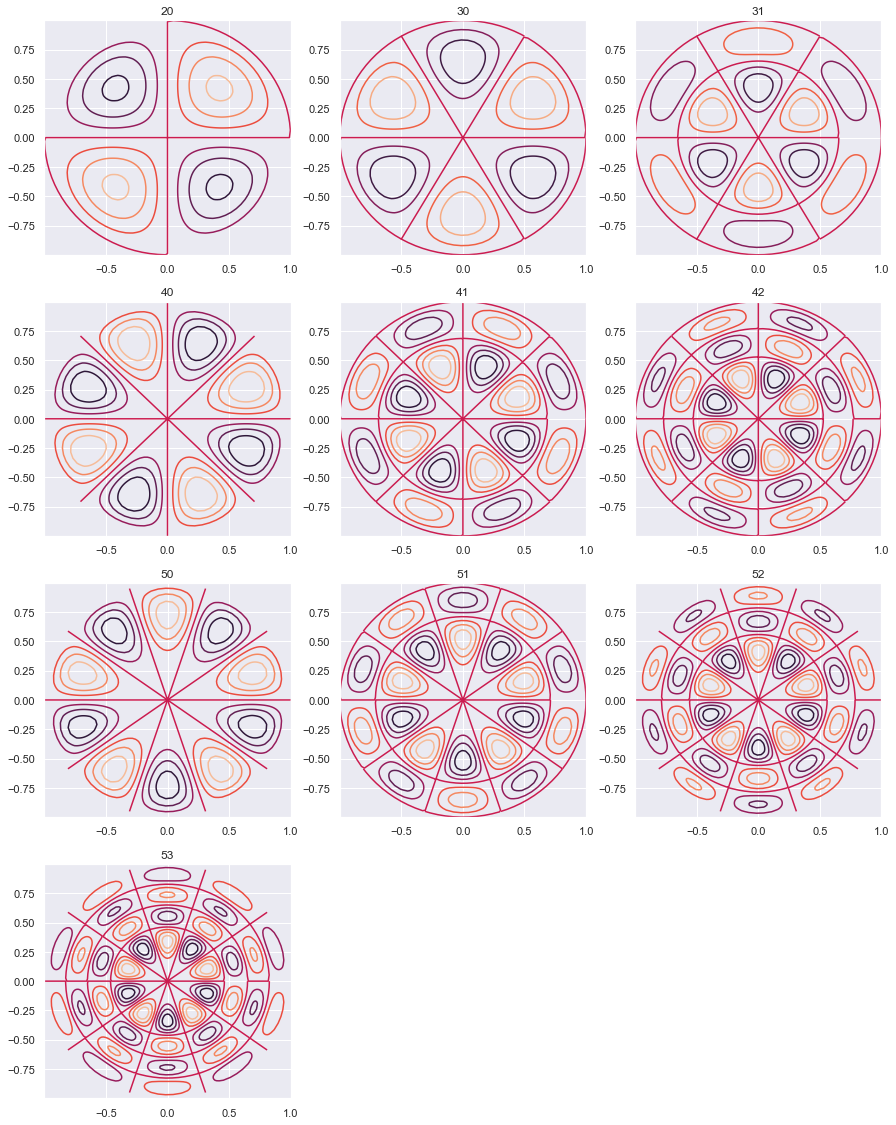
Oscillating Membrane (Multiplot)

plt.figure(figsize = [15,25])
k = 0
for n in range(6):
    for m in range(n-1):
        k = k+1
        z = np.array([displacement(n, m, rr, theta) for rr in r])

        plt.subplot(5,3,k)
        plt.title(str(n) + str(m))
        pylab.contour(x, y, z)
pylab.show()

png

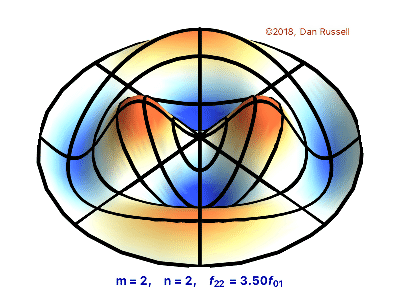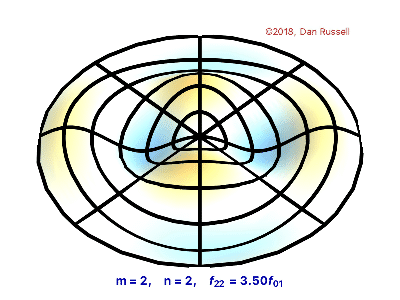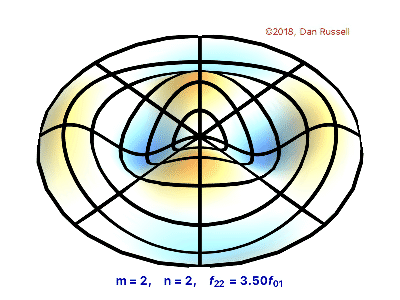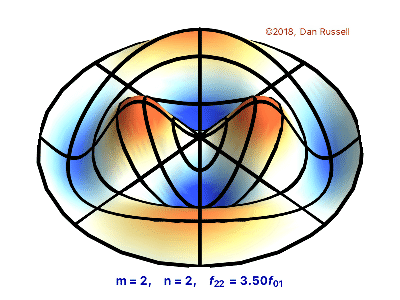
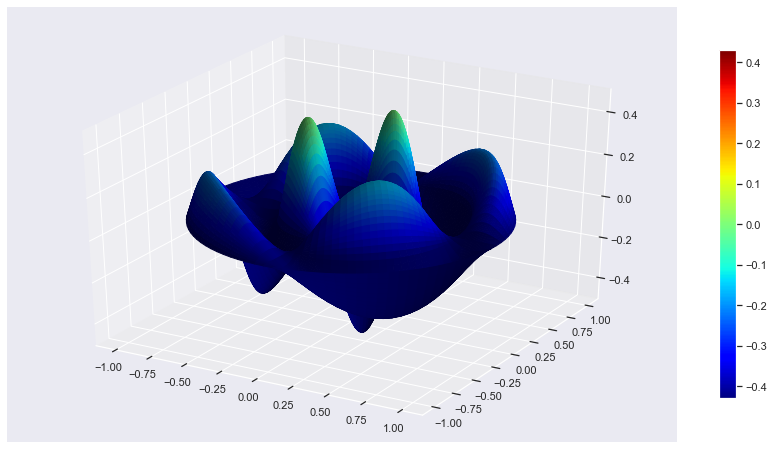
Oscilating Membrane ( m,n = 2,2)

n0,m0 = 2,2
r, theta = np.mgrid[0:1:100j, 0:2*np.pi:100j] 
x = r*np.cos(theta)
y = r*np.sin(theta)
z = displacement(n0, m0, r, theta)
N = z/(z.max() -z.min())
fig, ax = plt.subplots(subplot_kw=dict(projection='3d'), figsize=(15,8))
im = ax.plot_surface(x, y, z, rstride=1, cstride=1, facecolors=cm.jet(N))
mm = cm.ScalarMappable(cmap=cm.jet)
mm.set_array(R)    
fig.colorbar(mm, shrink=0.8);

png

References

  1. https://en.wikipedia.org/wiki/Vibrations_of_a_circular_membrane
  2. https://www.exoruskoh.me/single-post/2017/05/24/Vibrating-Membranes-and-Fancy-Animations
  3. https://www.acs.psu.edu/drussell/Demos/MembraneCircle/Circle.html
  4. http://balbuceosastropy.blogspot.com/2015/06/spherical-harmonics-in-python.html